One Dimensional Array
- Simplest data structure that makes use of computed address to locate its elements is the one- dimensional array or vector; number of memory locations is sequentially allocated to the vector.
- A vector size is fixed and therefore requires a fixed number of memory locations.
- Vector A with subscript lower bound of “one” is represented as below….
 |
| Add caption |
- L0 is the address of the first word allocated to the first element of vector A.
- C words are allocated for each element or node
- The address of Ai is given equation Loc (Ai) = L0 + C (i-1)
- Let’s consider the more general case of representing a vector A whose lower bound for it’s subscript is given by some variable b. The location of Ai is then given by Loc (Ai) = L0 + C (i-b)
Two Dimensional Array
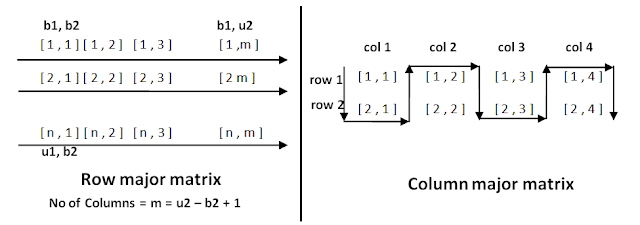
- Two dimensional arrays are also called table or matrix, two dimensional arrays have two subscripts
- Two dimensional array in which elements are stored column by column is called as column major matrix
- Two dimensional array in which elements are stored row by row is called as row major matrix
- First subscript denotes number of rows and second subscript denotes the number of columns
- Two dimensional array consisting of two rows and four columns as above Fig is stored sequentially by columns : A [ 1, 1 ], A [ 2 , 1 ], A [ 1 , 2 ], A [ 2 , 2 ], A [ 1 , 3 ], A [ 2 , 3 ], A [ 1, 4 ], A [ 2, 4 ]
- The address of element A [ i , j ] can be obtained by expression Loc (A [ i , j ]) = L0 + (j-1)*2 + i-1
- In general for two dimensional array consisting of n rows and m columns the address element A [ i , j ] is given by Loc (A [ i , j ]) = L0 + (j-1)*n + (i – 1)
- In row major matrix, array can be generalized to arbitrary lower and upper bound in its subscripts, assume that b1 ≤ I ≤ u1 and b2 ≤ j ≤u2
- For row major matrix : Loc (A [ i , j ]) = L0 + ( i – b1 ) *(u2-b2+1) + (j-b2)